Demystifying the Confusion Matrix

A simple 2x2 table can contain insightful metrics that enhance your decision-making.

7 min read Ben Hayes

Confusion Matrix

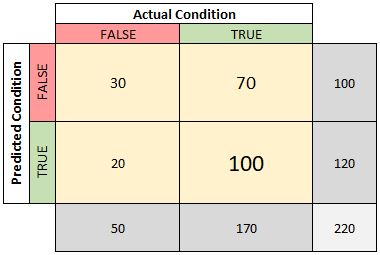
This is a 2x2 example of a confusion matrix. Notice that along one axis we have the actual outcome (what class did each observation actually belong to?) and along the other we have the predicted outcome. In each cell we have the count of observations that match the axes criteria. The count of observations that were predicted as false and actually are false was 30. The count of observations that were predicted as true and actually are false was 20. These counts will be instrumental when determining how effective a predictive model was given the context.

A few notes about confusion matrices that you should be aware of:

  • You may also hear them referred to as cross-tabulation or 2x2 tables.
  • The table can have different dimension sizes (e.g., 3x3, etc.).
  • The 'Actual' and 'Predicted' conditions may be flipped depending on the publisher.

Metrics

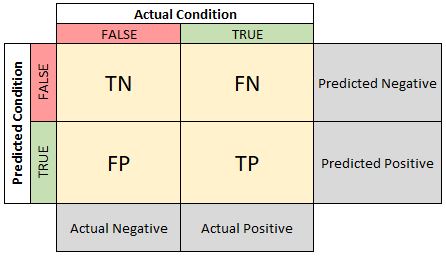
Now that we know what comprises the confusion matrix, we can begin to look closer at how the values provided can be evaluated to determine the effectiveness of our model. For the following analyses, we will use the more general confusion matrix where the counts have been replaced with “TP” for True Positives, “TN” for True Negatives, etc.

1. Prevalence

One of the key indicators of the confusion matrix, if not already known, is the prevalence. This value indicates how many true or positive cases actually occurred out of all of the observations. To calculate this value, divide all of the (actual) true observations with the total number of observations.

$$Prevalence = {Actual\;Positive \over Total\;Observations}$$ $$Prevalence = {FN + TP \over TN + FP + FN + TP}$$


2. Accuracy & Misclassification Rate

After understanding the prevalence, the next basic metric that can be derived is the prediction accuracy. Instead of dividing the count of actual true values, we divide the count of correct predictions by the total number of observations.

$$Accuracy = {True\;Predictions \over Total\;Observations}$$ $$Accuracy = {TN + TP \over TN + FP + FN + TP}$$

Alternatively, you can find the misclassification rate which indicates how often your model was wrong. Instead of looking at the correct predictions, we divide the count of incorrect predictions by the total number of observations.

$$Misclassification\;Rate = {False\;Predictions \over Total\;Observations}$$ $$Misclassification\;Rate = {FP + FN \over TN + FP + FN + TP}$$

You may have noticed that summing accuracy and misclassification rate will equal 1 or alternatively:

$$1 - Accuracy = Misclassification\;Rate$$ $$1 - Misclassification\;Rate = Accuracy$$


The next four sets of metrics move away from the overall performance of the model and look at different ways of measuring predictive power (or lack thereof). This means we will not only be changing the numerator but also the denominator in each formula. Grasping these subtle differences is critical as they dramatically alter our interpretation of each.


3. True Positive Rate (Recall, Sensitivity) & False Negative Rate

The true positive rate (also known as recall or sensitivity) is an important metric as it indicates of all of the actual positive cases, how many did we successfully identify as positive. In other words, we want to know the number of positive cases we successfully recalled as positive cases. To calculate, divide the number of true positives by the number of actual positive cases.

$$True\;Positive\;Rate = {True\;Positives \over Actual\;True}$$ $$True\;Positive\;Rate = {TP \over TP + FN}$$

We can evaluate the false negative rate where we want to know how frequently we incur false negatives (predicted negative but actually positive).

$$False\;Negative\;Rate = {False\;Negatives \over Actual\;True}$$ $$False\;Negative\;Rate = {FN \over TP + FN}$$

The true positive rate added with the false negative rate equals 1.

$$1 = True\;Positive\;Rate + False\;Negative\;Rate$$


4. False Positive Rate (Miss rate) & True Negative Rate (Specificity)

The false positive rate (do not confuse with false negative rate!) is also known as the miss rate (do not confuse with misclassification rate!). In other words, the false positive rate indicates how often we predict an actual negative observation to be true.

$$False\;Positive\;Rate = {False\;Positives \over Actual\;False}$$ $$False\;Positive\;Rate = {FP \over TN + FP}$$

We can also evaluate the associated metric called the true negative rate (also known as specificity) which indicates how often we correctly classify negative cases.

$$Specificity = {True\;Negatives \over Actual\;False}$$ $$Specificity = {TN \over TN + FP}$$

You may have identified a pattern here: false positive rate plus specificity (TNR) equals 1.

$$1 = False\;Positive\;Rate + Specificity$$


5. Positive Predictive Value (Precision) & False Discovery Rate

The positive predictive value (also known as precision) of our model will indicate how often we correctly classify an observation as positive when we predict positive. To calculate PPV we divide the number of correct positive guesses by the total number of positive guesses.

$$Precision = {True\;Positive \over Predicted\;Positive}$$ $$Precision = {TP \over TP + FP}$$

Alternatively, we can calculate the false discovery rate which indicates when we predict positive, how often are we incorrect.

$$False\;Discovery\;Rate = {False\;Positives \over Predicted\;Positive}$$ $$False\;Discovery\;Rate = {FP \over TP + FP}$$

And yes, adding false discovery rate and precision will sum to 1.

$$1 = Precision + False\;Discovery\;Rate$$


6. Negative Predictive Value & False Omission Rate

The negative predictive value (apparently doesn’t deserve a nickname and) indicates how often we are correct (true) when we predict an observation to be negative.

$$Negative\;Predictive\;Power = {True\;Negatives \over Predicted\;Negative}$$ $$Negative\;Predictive\;Power = {TN \over TN + FN}$$

If we want to know how often we are incorrect when we predict a value to be negative, we can evaluate the false omission rate.

$$False\;Omission\;Rate = {False\;Negatives \over Predicted\;Negative}$$ $$False\;Omission\;Rate = {FN \over TN + FN}$$

Adding the negative predictive value with the false omission rate will sum to 1.

$$1 = Negative\;Predictive\;Value + False\;Omission\;Rate$$

Plotting These Values To Aid Decision Making

Now that you understand the common metrics derived from the confusion matrix, we should explore two popular graphs that can be generated from the metrics (there are others but we will stick with these two for now).

Receiver Operating Characteristic (ROC) Curve

An ROC Curve plots True Positive Rate (Sensitivity) against False Positive Rate (1 minus Specificity). This curve is instrumental when deciding what classification cutoff may be appropriate to use as tradeoffs in sensitivity and specificity can be seen. A term commonly used when evaluating an ROC Curve is the area under the curve (AUC). A perfect classifier has an AUC equal to 1 while a classifier which relies on a coin-flip has an AUC equal to 0.5.

An example from my post on predicting criminal recidivism is shown below:

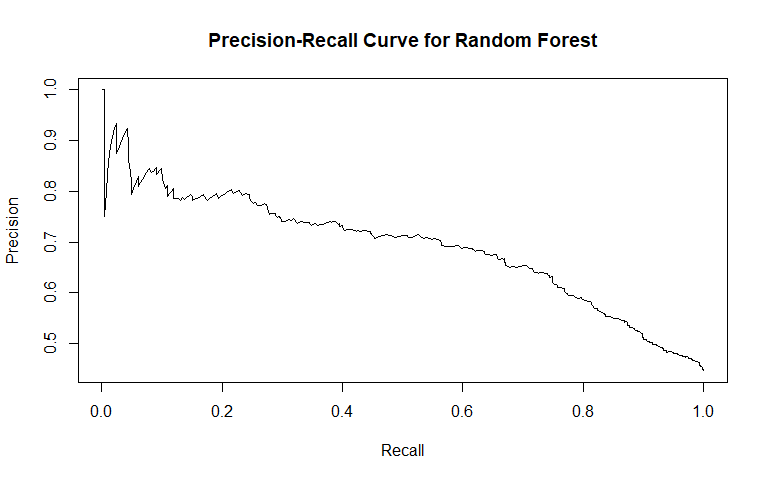
Precision-Recall Curve

A Precision-Recall Curve is a supplemental graph which can help identify appropriate cutoffs as well. Recall (Sensitivity, TPR) is plotted along the X-axis and precision (PPV) is plotted along the Y-axis. One note about precision-recall curves is that they do not account for true negatives. In other words, a model is not rewarded visually by a precision-recall curve for correctly identifying negative cases. Generally a curve with higher precision (Y-axis) is preferred although lines can cross-over multiple times.

An example from my post on predicting criminal recidivism is shown below:

Summary

Understanding these metrics takes time and practice. The names sound similar but the interpretations have stark contrasts with each other. Understanding when to rely on one metric over another takes even more time because, in most problem contexts, the cost of a false positive does not equal the cost of a false negative.

  • Prevalence indicates how frequent positive cases occur in your sample.
  • Accuracy indicates of all observations how many were correctly classified (TP, TN). Misclassification rate indicates of all observations how many were incorrectly classified.
  • Sensitivity (TPR, Recall) indicates how many of the positive observations were correctly identified as positive. False negative rate indicates how many of the positive observations were incorrectly identified as negative.
  • False positive rate indicates how many of the negative observations were incorrectly identified as positive. True negative rate indicates how many of the negative observations were correctly identified as negative.
  • Precision (PPV) indicates how many of your positive predictions were correct. False discovery rate indicates how many of your positive predictions were incorrect.
  • Negative predictive value (NPV) indicates how many of your negative predictions were correct. False omission rate indicates how many of your negative predictions were incorrect.

This simple 2x2 table can provide valuable insight into the performance of your predictive model.

Additional Sources

The Wikipedia article on the Confusion Matrix concept contains the majority of information mentioned above and helped me grasp the subtle differences in the matrix’s metrics (say that 5 times fast).